Thermodynamics

Thermodynamics

NCERT Summary

1. Thermodynamic Equilibrium

• Temperature of a body is related to its average internal energy, not to kinetic energy of motion of centre of mass.
• Equilibrium in thermodynamics refer to situation when macroscopic variables defining thermodynamic state of system don’t’ depend on time.

2. Zeroth Law of Thermodynamics

• Two system in thermal equilibrium with third system separately are in thermal equilibrium with each other.
• If T_A = T_C and T_B = T_C then T_A = T_B
• Thermodynamic variable whose value is equal for two systems in thermal equilibrium is called temperature.

3. Heat,Internal Energy and Work

• Heat is energy transfer arising due to temperature difference between system and surroundings.
• Internal energy is simply the sum of kinetic energies and potential energies of the molecules in the frame of reference to which centre of mass of system is at rest.
• Internal energy depends on state of the system, not how the state was achieved.
• There are two ways to change internal energy of a thermodynamic system.

           a. To do work on system

           b. Supply heat to system

          So heat and work are two modes of altering the state of a thermodynamic system and          changing internal energy.

• Heat and work in thermodynamics are not state variables.
• U is a state variable. \(\Delta \)V depends only on initial and final states and not on path taken by gas to go from one to another.
• \(\Delta \)Q and \(\Delta \)W will depend on path taken to go from initial to final state.
• Work done during thermodynamic process \(\Delta W=\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{PdV}\)
• Area under the P – V diagram with the volume axis gives the work done in thermodynamic process.

4. Specific Heat Capacity

• Molar specific heat at constant volume.

           \({{c}_{V}}={{\left( \frac{\Delta Q}{\Delta T} \right)}_{v}}=\left( \frac{\Delta V}{\Delta T} \right)\)

• Molar specific heat at consant pressure.

           \({{C}_{P}}={{\left( \frac{\Delta Q}{\Delta T} \right)}_{P}}={{\left( \frac{\Delta U}{\Delta T} \right)}_{P}}+{{\left( \frac{\Delta V}{\Delta T} \right)}_{P}}\)

           \(PV=RT \, \, \, \, \therefore P{{\left( \frac{\Delta V}{\Delta T} \right)}_{P}}=R\)

• \({C_P} = {C_V} + R\) (MAYER’S Equation)
• \(\gamma =\cfrac{{{C}_{P}}}{{{C}_{v}}}=\cfrac{{{C}_{v}}+R}{{{C}_{v}}}=1+\cfrac{R}{{{C}_{v}}}\)                \({{C}_{P}}=\gamma \times {{C}_{V}}\)

5. First Law of Thermodynamics

• \(\Delta Q=\Delta U+\Delta W\) (Energy conservation law)

           \(\Delta Q\)=heat supplied to system by the surrounding

           \(\Delta W\)=work done by the system on the surrounding

           \(\Delta U\)=Change in internal energy of a the system

• Heat supplied to system goes in partly to increase internal energy and rest in work on environment.
• This is simply the general law of conservation of energy applied to any system in which energy transfer is taken into account.
• \(\Delta W=P\Delta V\)

           \(\therefore \Delta Q=\Delta U+P\Delta V\)

6. Thermodynamic State Variables

• Thermodynamic state variables describe equilibrium state of system. These state variables are not necessarily independent.
• The connection among state variables is called equation of state.
• Equilibrium state of thermodynamic system is described by state variables. The value of state variable depends on particular state not by the path used to arrive that state. Pressure, volume, temperature and mass are state variable. Heat and work are not state variables.
• For an ideal gas, equation of state is \(PV = {\mu}RT\)
• Thermodynamic state variables are of two types

           a. Extensive

           b. Intensive

• Extensive variables indicates size of system.
• Internal energy, volume and mass are extensive variables, but pressure, temperature and density are intensive variables.

7. Reversible and Irreversible Process

• Spontaneous processes in nature are irreversible.
• A process is reversible if the process can be turned back such that both the system and surrounding return to their original states with no any other change anywhere else in universe.
• A quasi-static isothermal expansion of an ideal gas in a cylinder fitted with a frictionless movable piston is a reversible process.
• A quasi-static process is an infinitely slow process such that system remains in thermal and mechanical equilibrium with surroundings throughout. In this process pressure and temperature of the environment can differ from those of system only infinitesimally.

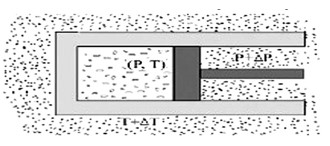
                             No accelerated motion of piston

8. Thermodynamic Processes

• A thermodynamic process is an activity where a thermodynamic system is taken from one equilibrium state to another.
• Reversible process
• Irreversible process
• Cyclic process

9. Isothermal Process

• For isothermal processes Temperature during the process should be constant

           PV = constant

• So pressure of given mass of a gas varies inversely as its volume.
• Work done in isothermal process.

           If a system of ideal gas at temperature T goes from (P₁, V₁) to (P₂, V₂) equilibrium state, then           work done

           \(W=\mu RT\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)=\mu RT\ln \left( \frac{{{P}_{1}}}{{{P}_{2}}} \right)\)

• Here \(\Delta T=0  \, \, \, \, \, \, \, \,   \therefore \Delta U=0\)

           \(\Delta Q=\Delta W\,\,=\mu RT\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\)

10. Adiabatic Process

• In adiabatic process heat interaction between system and surrounding is zero i.e. \(\Delta Q=0\)
• PV^x = constant

          Where \(\gamma \) = ratio of molar specific heats at constant pressure and at constant volume.

• System is insulated from surroundings and heat absorbed or releases is zero.
• Work done by gas results in decrease in its internal energy
• If system change from (P₁, V₁, T₁) to (P₂, V₂, T₂)

           \(\Delta W\,\,=\frac{\mu R({{T}_{1}}-{{T}_{2}})}{\gamma -1}=\frac{({{P}_{1}}{{V}_{1}}-{{P}_{2}}{{V}_{2}})}{\left( \gamma -1 \right)}\,\,where\,\,\gamma ={{C}_{p}}/{{C}_{v}}\)

• If work done by gas ( W > 0), then T₂ < T₁.

11. Isobaric Process

• For isobaric process pressure during the process should be constant

           \(\frac{V}{T}=\text{constant}\)

• Work done in isobaric process

           \(W=P\left( {{V}_{2}}-{{V}_{1}} \right)=\mu R\left( {{T}_{2}}-{{T}_{1}} \right)\)

• Heat partly to do absorbed goes partly to increase internal energy and mechanical work.

          \(\Delta Q=\Delta U+\Delta W\)

          \(\Delta U=\mu {{C}_{v}}\Delta T,\Delta Q=\mu {{C}_{v}}\Delta T\,\,and\,\,\Delta W=\mu R\Delta T\)

          \(\cfrac{\Delta W}{\Delta Q}=\cfrac{R}{{{C}_{P}}}=\cfrac{\gamma -1}{\gamma }\,\,and\,\,\cfrac{\Delta U}{\Delta Q}=\cfrac{{{C}_{v}}}{{{C}_{P}}}=\cfrac{1}{\gamma }\)

12. Isochoric Process

• For isochoric process volume during the process should be constant

          \(\frac{P}{T}= \text{constant}\)

• Work done in isochoric process, \(\Delta W=P\Delta V=0\)
• \(\Delta Q=\Delta U=\Delta W\)

           \(\Delta Q=\Delta U\)

• Heat absorbed by gas goes entirely to change its internal energy and its temperature.
• Change in internal energy is determined by specific heat at constant volume and temperature change

13. Cyclic Process

• In any cyclic process system returns to initial state, \(\Delta U=0\)
• Hence total heat absorbed equals the work done by the system, \(\Delta Q=\Delta W\)

14. Heat Engine

• Heat engine is a device in which a system undergoes a cyclic process resulting in conversion of heat in to the sink.

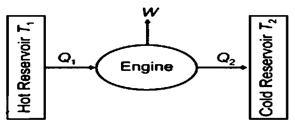
• Efficiency of the engine is

          \(\eta \frac{W}{{{Q}_{1}}}=\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\)

           Q₁ = heat absorbed from source

          Q₂ = heat released to sink

          \(\eta \) = efficiency of heat engine

• Heat engine based on idealized reversible processes achieve the highest possible efficiency.

15. Refrigerator

• A refrigerator is the reverse of a heat engine. Working substance extracts heat from cold reservoir, some external work is done on system and heat is released to reservoir at high temperature.
• Coefficient of performance of refrigerator \(\frac{heat\,\,extracted}{work\,\,input}\)

           \(\beta =\frac{{{Q}_{2}}}{W}=\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}=\frac{{{T}_{2}}}{\left( {{T}_{1}}-{{T}_{2}} \right)}=\frac{1-\eta }{\eta }\)

• Coefficient of performance for heat pump is

           \(\beta =\frac{{{Q}_{1}}}{W}=\frac{{{T}_{1}}}{{{T}_{1}}-{{T}_{2}}}=\frac{1}{\eta }\)

16. Second Law of Thermodynamics

• Kelvin-Planck statement: No process is possible whose sole result is absorption of heat from a reservoir and complete conversion of heat into work
• Clausius statement: No process is possible whose sole result is transfer of heat from cold reservoir to hotter object.
• Two statements are completely equivalent.
• It shows that efficiency of a heat engine can never be unity so heat released to cold reservoir can never be made zero.
• Kelvin Planck and Clausius deny the prefect heat engine and refrigerator.

17. Carnot Engine

• Carnot engine is a reversible engine operating between two temperature T₁ and T₂. Cannot cycle consists of two isothermal and two adiabatic processes. Its efficiency is
• Engine efficiency of Carnot engine does not depend on nature of working substance.

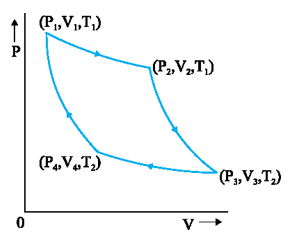
                   \(\eta =1-\frac{{{T}_{1}}}{{{T}_{2}}}\)

• Carnot Theorem: Any other engine working between temperature T₁ and T₂ cannot have efficiency more than that of Carnot engine. The Carnot engine’s efficiency is independent of nature of working substance. In Carnot cycle \(\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}\) is universal relation and this relation can be used to design universal thermodynamic scale.